Maple Financial Modeling Toolbox doplňuje víceoborové matematické prostředí systému Maple více než 100 novými příkazy, které jsou výslovně určeny pro kvantitativní finanční modelování a analýzy. Tyto nové možnosti lze velmi efektivně kombinovat se stávajícími vlastnostmi systému Maple, včetně ODR a PDR řešičů, statistické analýzy dat a optimalizace, a tím lze vytvářet analytické aplikace a modely v rámci interaktivního dokumentačního prostředí systému Maple.
Oblasti pro aplikace
- Analýza rizik
- Portfolio managementu
- Kvantitativní analýzy
- Validace modelů a jejich vetování
- a mnohé další…
Klíčové vlastnosti toolboxu
- Interaktivní technické rozhraní dokumentu s intuitivním 2D editorem rovnic pro zachycení a znovupoužití znalosti jako informační výhody
- Nástroje pro vytváření a analýzu časového vývoje úrokových sazeb
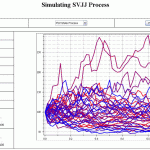
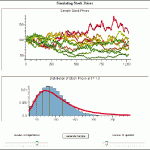
- Náhodné procesy a simulace, symbolické nástroje pro práci s náhodnými proměnnými
- Sazby pro krátkodobé pojišťovací modely a analytické vzorce
- Plný přístup k funkčnosti Maple, včetně možnosti práce s ODR a PDR, včetně řešičů DAE, navíc k lineární a nelineární optimalizaci
- Metody a nástroje pro konstrukci binomických a trinomických stromů
Detaily vybraných klíčových vlastností
Interaktivní prostředí
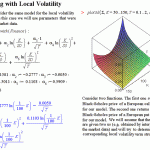
- Plně dokumentované komponenty (texty, obrázky, atd.), které začleňují matematické vzorce plně do technického dokumentu a zlepšují čitelnost a možnosti uchopení a simulace problému.
- Intuitivní a názorné vkládání matematických objektů.
Přístup k jádru systému Maple
Řešiče pro ODR, PDR, DAE, statistika, optimalizace a mnoho dalších knihoven. Zkvalitněné grafické prostředí a editační možnosti výsledných grafů pro pokročilou vizualizaci. Možnost generování kódu do několika jazyků: C, FORTRAN, Visual Basic®, Java™, MATLAB®.
Sady odborných příkazů
Nástroje pro vytváření a analýzu termínování úrokových sazeb. Náhodné procesy, práce s náhodnými proměnnými, symbolické výpočty a simulace jako např.: Brownův pohyb, Geometrický Brownův pohyb, Ornstein-Uhlenbeck proces, Gauss-Markovův proces, Poisson a Gamma proces a mnoho dalších.